На что похоже падение в черную дыру? Что вы увидите?

Вселенная по-разному уничтожает что-либо. Если вы попытаетесь задержать дыхание в космосе, ваши легкие взорвутся; если вместо этого вы вдохнете каждую молекулу воздуха, вы потеряете сознание. В некоторых местах вы замерзнете, лишившись последнего тепла своего тела; в других будет настолько жарко, что атомы вашего тела превратятся в плазму. Но из всех способов, которыми Вселенная избавляется от объектов, самый увлекательный — отправить его в черную дыру.

Что находится за горизонтом событий?

Согласно нашей теории гравитации — общей теории относительности Эйнштейна — свойства черной дыры определяются тремя вещами. А именно:

1. Масса, или общее количество вещества и эквивалентное количество энергии (по формуле E = mc²), которые идут на формирование и рост черной дыры до ее текущего состояния.
2. Заряд, или общий электрический заряд, который существует в черной дыре от всех положительно и отрицательно заряженных объектов, которые попали в черную дыру за всю историю ее жизни.
3. Угловой импульс (момент), или спин, который является мерой общего количества вращательного движения, которое черная дыра имеет по своей природе.

В реальности, все черные дыры, которые физически существуют в нашей Вселенной, должны иметь большие массы, значительное количество угловых моментов и незначительные заряды. Это чрезвычайно усложняет ситуацию.

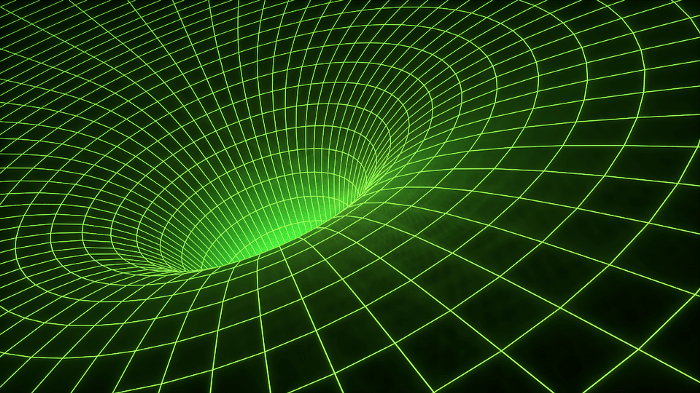
Когда мы обычно представляем черную дыру, мы воображаем простой ее вариант, который описывается только ее массой. У него есть горизонт событий, окружающий одну точку, и область, окружающая эту точку, за пределы которой свет не может выйти. Эта область совершенно сферическая и имеет границу, разделяющую области, из которой свет может вырваться и из которой не может: горизонт событий. Горизонт событий находится на определенном расстоянии (радиус Шварцшильда) от сингулярности во всех направлениях одновременно.

Это упрощенная версия реалистичной черной дыры, но прекрасное место, с которого можно начать размышлять о физике, происходящей в двух разных местах: за горизонтом событий и внутри горизонта событий.

За пределами горизонта событий гравитация ведет себя так, как вы обычно ожидаете. Пространство искривляется в присутствии массы, что заставляет каждый объект во Вселенной испытывать ускорение в направлении центральной сингулярности. Если бы вы оказались на большом расстоянии от черной дыры в состоянии покоя и позволили предмету упасть в нее, что бы вы увидели?

Если предположить, что вам удалось сохранить неподвижность, вы увидите, как падающий объект медленно ускоряется от вас к этой черной дыре. Он ускорится к горизонту событий, после чего произойдет нечто странное. Вам покажется, что он замедляется, затухает и становится краснее. Но он не исчезнет полностью. Он лишь приблизится к этому: станет тусклым, красным и сложнее обнаружимым. Вы всегда сможете его увидеть, если будете смотреть достаточно пристально.

Теперь вообразим тот же сценарий, но в этот раз представим, что вы и есть тот самый падающий в черную дыру объект. Опыт происходящего будет совершенно другим.

Горизонт событий будет становится больше гораздо быстрее, чем вы ожидали, поскольку искривление пространства будет становится сильнее. Вокруг горизонта событий пространство настолько искривлено, что вы увидите множество изображений вселенной, которая находится извне, словно ее отразили и перевернули.

И как только вы пересечете горизонт событий, вы не только все еще сможете видеть внешнюю вселенной, но и часть вселенной внутри горизонта событий. В последние моменты пространство будет выглядеть совершенно плоским.

Что находится в черной дыре?

Физика всего этого сложна, но вычисления довольно просты и элегантнее всего выполнены Эндрю Хэмилтоном из Университета Колорадо в серии работ конца 2000-х — начала 2010-х годов. Хэмилтон также создал серию впечатляющих визуализаций того, что вы увидите, упав в черную дыру, основываясь на этих расчетах.

[embedded content]

Изучив эти результаты, мы можем извлечь ряд выводов, многие из которых нелогичны. Чтобы попытаться их осмыслить, нужно изменить способ представления пространства. Обычно мы думаем о нем как о неподвижной ткани и считаем, что наблюдатель куда-то «спускается». Но внутри горизонта событий вы всегда в движении. Пространство движется — как беговая дорожка — непрерывно, перемещая все в себе к сингулярности.

И оно перемещает все так быстро, что даже если вы ускоритесь прямо от сингулярности с бесконечной силой, вы все равно упадете к центру. Объекты, находящиеся за пределами горизонта событий, все так же будут посылать вам свет со всех сторон, но вы сможете увидеть лишь часть объектов из-за горизонта событий.

Линия, которая определяет границу между тем, что может увидеть любой наблюдатель, математически описывается кардиоидой, где компонент с наибольшим радиусом касается горизонта событий, а компонент наименьшего радиуса оказывается в сингулярности. Это значит, что сингулярность, даже будучи точкой, не обязательно связывает все, что в нее попадает, со всем остальным. Если вы и я упадем в горизонт событий с разных сторон одновременно, мы никогда не увидим свет друг друга после того, как произойдет пересечение горизонта событий.

Причиной этого является постоянно движущаяся ткань самой Вселенной. Внутри горизонта событий пространство движется быстрее света, поэтому ничто не может вырваться из черной дыры. Вот почему, попав в черную дыру, вы начинаете видеть странные вещи вроде нескольких изображений одного и того же объекта.

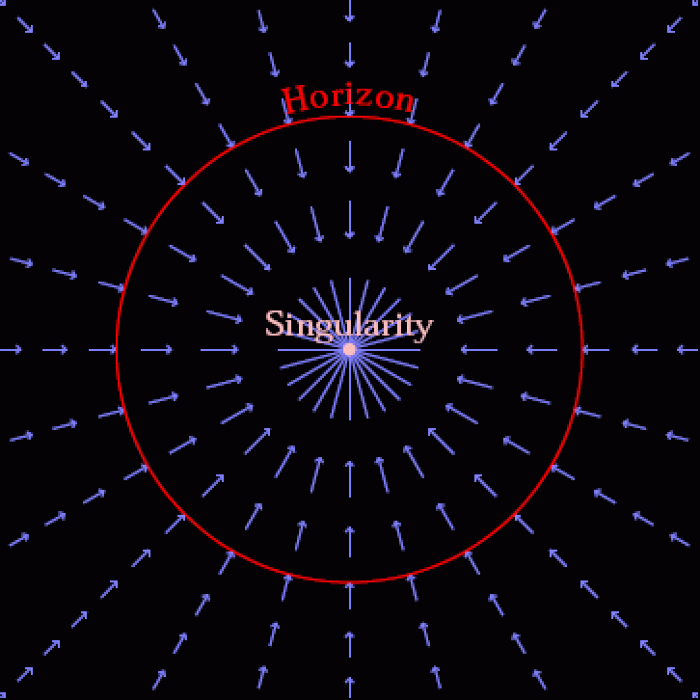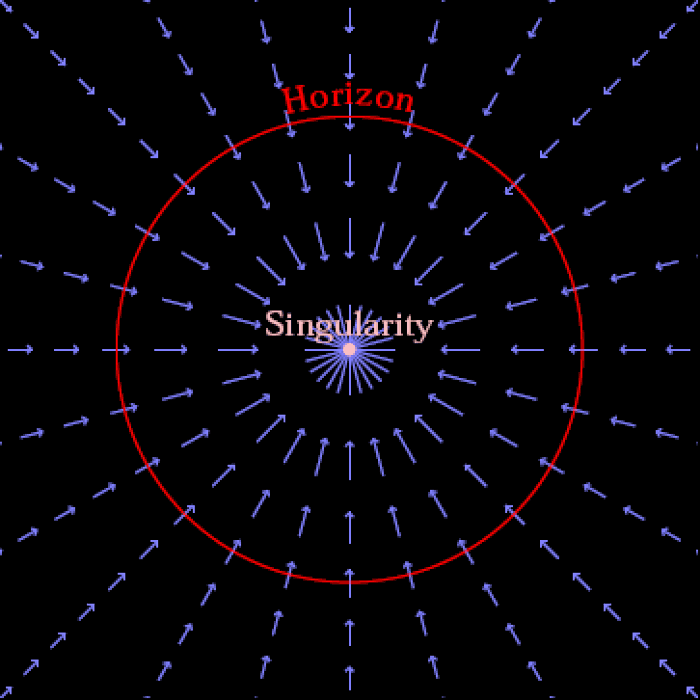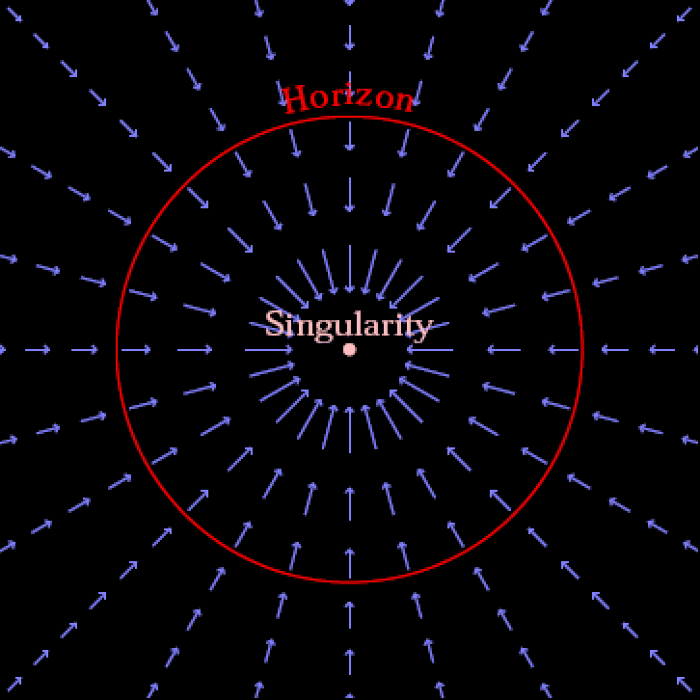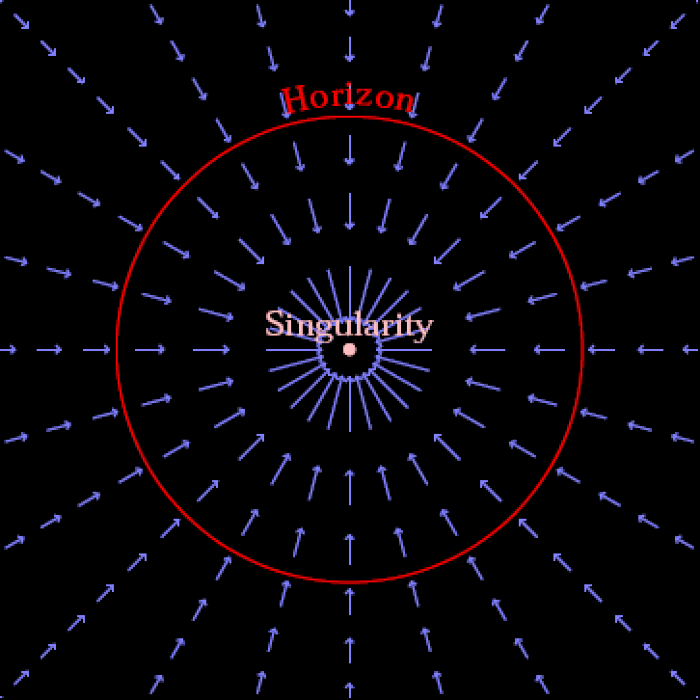
Можно понять это, задав вопрос: где сингулярность?

Изнутри горизонта событий черной дыры, в каком направлении вы бы ни двигались, вы в конечном итоге сталкиваетесь с самой сингулярностью. Поэтому, как ни странно, сингулярность появляется во всех направлениях. Если ваши ноги указывают в направлении ускорения, вы увидите их перед собой, но также и над собой. Все это легко просчитывается, хоть и чрезвычайно нелогично. И это только для упрощенного случая: невращающейся черной дыры.

А теперь давайте перейдем к физически интересному случаю: когда черная дыра вращается. Черные дыры обязаны своим происхождением системам из вещества — вроде звезд — которые всегда вращаются на каком-то уровне. В нашей Вселенной (и в общей теории относительности) угловой момент представляет собой абсолютную заключенную величину для любой закрытой системы; нет никакого способа от него избавиться. Когда совокупность вещества коллапсирует до радиуса, который меньше радиуса горизонта событий, угловой момент оказывается заключенным внутри него, как и масса.

Решение, которое мы имеем здесь, будет намного сложнее. Эйнштейн представил общую теорию относительности в 1915 году, а Карл Шварцшильд получил решение по невращающейся черной дыре пару месяцев спустя, в начале 1916 года. Но следующий шаг в моделировании этой проблемы более реалистичным способом — когда черная дыра обладает угловым моментов, а не только массой — был предпринят только в 1963 году, когда Рой Керр нашел точное решение в 1963 году.

Существует несколько фундаментальных и важных различий между более наивным и простым решением Шварцшильда и более реалистичным и сложным решением Керра. Среди них:

• Вместо единого решения о том, где находится горизонт событий, у вращающейся черной дыры есть два математических решения: внутренний и внешний горизонт событий.
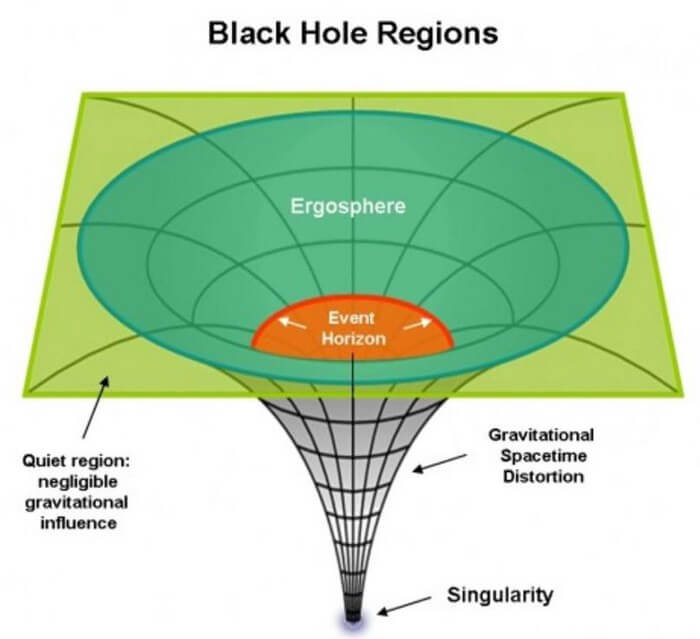
• За пределами даже внешнего горизонта событий существует место, известное как эргосфера, в котором само пространства перемещается со скоростью вращения, равной скорости света, и частицы в нем испытывают огромные ускорения.
• Существует максимальное допустимое отношение углового момента к массе; если импульс будет слишком сильным, черная дыра будет излучать эту энергию (посредством гравитационного излучения), пока он не упадет до предела.
• И самое интересное: сингулярность в центре черной дыры — это уже не точка, а одномерное кольцо, радиус которого определяется массой и угловым моментом черной дыры.

Учитывая все это, что произойдет, когда вы попадете в черную дыру? Да то же самое, что произойдет, если вы попадете в невращающуюся черную дыру, за исключением того, что все пространство не ведет себя так, будто падает в направлении центральной сингулярность. Вместо этого, пространство также ведет себя так, будто перемещается вдоль направления вращения, как закручивающаяся воронка. Чем больше отношение углового момента к массе, тем быстрее она вращается.

Это означает, если вы видите, как что-то падает в черную дыру, вы увидите, что оно становится более тусклым и красным, но также размазанным в кольцо или диск по направлению вращения. Если вы упадете в черную дыру, вас закрутит, как на карусели, которая притягивает вас к центру. И когда вы достигнете сингулярности, она будет кольцом; разные части вашего тела встретятся с сингулярностью — на внутренней эргоповерхности черной дыры Керра — в разных пространственных координатах. Вы постепенно перестанете видеть другие части вашего собственного тела.

Самое важное, что вы должны уяснить из этого всего — это то, что ткань самого пространства находится в движении, а горизонт событий определяется как место, в котором даже если вы будете двигаться на скорости света, какое бы направление вы ни выбрали, вы неизбежно столкнетесь с сингулярностью.

Визуализации Эндрю Хэмилтона — это наилучшие и самые точные модели того, что происходит при падении в черную дыру, и настолько нелогичные, что их нужно просматривать снова и снова, пока не начнешь что-то понимать (на самом деле не начнешь). Это жутко и красиво, и если вы достаточно авантюрны, чтобы когда-либо прилететь к черной дыре и пересечь горизонт событий, это будет последним, что вы когда-либо видели.

Попробуете? Расскажите в нашем чате в Телеграме.